AVL Tree 是一種二元搜尋樹(Binary search tree)實做方式，大部分的實做方式與二元搜尋樹一樣，差異在於AVL tree在過程中會透過計算並調整樹的結構來讓樹維持平衡，而不會導致二元搜尋樹不平衡。由於整個樹不會長歪，在搜尋時的速度會更快。

AVL Tree為對於每一個左子節點的高度和右子節點的高度，兩者之間的差異必須在正負1之間。

AVL 樹的不平衡點調整之四種型式 

1. 若A在B的左邊的左邊，則為LL型。
   
2. 若A在B節點的右邊的右邊，則為RR型。

若A在B節點的左邊的右邊，則為LR型。

若A在B節點的右邊的左邊，則稱為RL型。

​​​​​​​

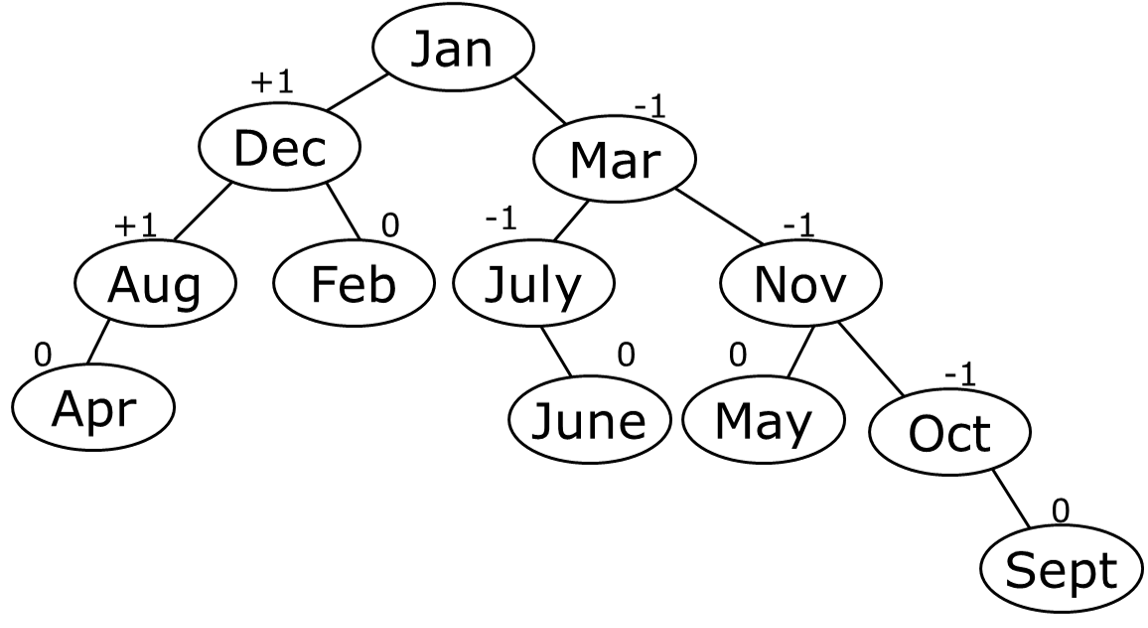
Insert the following data into the empty AVL tree, “Mar,May,Nov,Aug,Apr,Jane,Dec,July,Feb,June,Oct,Sept”

​​​​​​​